Investigation of the elastic behavior of reciprocal systems using homogenization techniques – L. Greco et al. (2013)

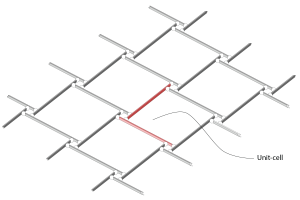
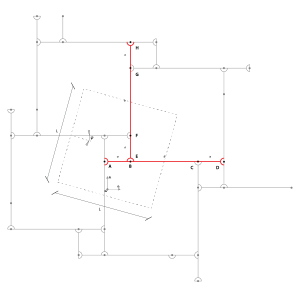
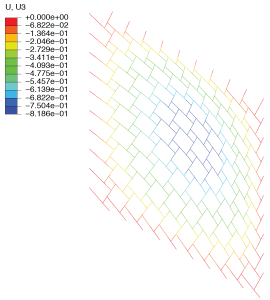
In this paper, the authors endeavour to develop design formulas for reciprocal systems using homogenization techniques. The theoretical background for homogenizing periodic beams systems as Kirchhoff-Love plates is first recalled. Then it is applied to a square reciprocal system. It is found that only biaxial bending (i.e. positive Gaussian curvature) generates stress inside the beams so that the equivalent plate model is a degenerated Kirchhoff-Love which is fully detailed. Then, some optimal configurations are investigated in terms of bending stiffness and strength. Finally, in order to validate the approach, full finite element simulations of simply supported reciprocal systems on square boundaries are compared with the homogenized solution previously derived. The convergence of the model and its accuracy for reasonable scale ratio is confirmed.

Media